Alexander Grothendieck, the secret genius of mathematics

This is an English translation of a post written in French by my father Gérard Lebrun. The pages numbers refer to the original text of Grothendieck’s work Récoltes et Semailles (“Crops and Seeds”).

I was intrigued by the unusual path of Grothendieck, the recently deceased mathematician genius who, after twenty years of work that garnered him the 1966 Field Medal (the Nobel Prize for mathematicians) brutally severed all links with the mathematical community and lived for 45 years in seclusion and solitude, devoting himself to meditation, the search for meaning, and introspection. I tried to understand.

Outside the circle of mathematicians who are still exploring the paths opened by this visionary, there is little documentation on Grothendieck, except for an account written by his own hand, a kind of a diary that he kept (intimate and at the same time “extimate”, since he sent a few copies to former colleagues or former students, and considered publishing it at one point, but didn’t find a publisher) - a very long diary of over a thousand pages entitled “Crops and Seeds: Reflections and Testimony about my Past as a Mathematician.” Although unpublished then, the text has already been making its way to readers. I will quote a few excerpts from it, so that you can learn about and appreciate the ideas of a man in search of the absolute.

This post is divided into 3 parts:

I. A secret genius or some biography details

II. Accomplishments in mathematics

III. Break with the mathematical community: meaning and spirituality

The name of Grothendieck, a mathematician who died recently at the age of 86, is not very well-known or is completely unknown to the public. We are talking here about an extraordinary person who made a mark on the culture of his time - a lone genius who opened new unimagined paths in mathematics, not only one of the greatest scientists of the twentieth century, but also a libertarian spirit, a rebel, a nonconformist who brutally broke all ties with the mathematical community in 1970 at the height of his fame just like Rimbaud suddenly abandoned writing poetry. Rimbaud turned away from his muse and chose personal advancement over his art by getting into the coffee and gun trade; Grothendieck withdrew from society to live in solitude in a small village in the Pyrenees, not to escape from himself but to find himself in an insatiable spiritual quest that is documented in Crops and Seeds.

I. A secret genius #

Some key elements of a remarkable biography, along with quotes gleaned here and there from Crops and Seeds.

Alexander Grothendieck was born to a Russian-Jewish father, a revolutionary anarchist named Schapiro, and a German mother, a left-wing activist named Grothendieck (as you can see, he has his mother’s last name). His father was incarcerated from 1906 to 1917 for participating in the revolution against Czar Nicolas II. The couple emigrated to France as Hitler rose to power, leaving their child Alexander (he was six years old at the time) in Germany in the care of a foster family – with a pastor who practiced the Frénet method and promoted the “back to the land” movement.

It was in 1933, when I was six years old that the first turning point in my life occurred; it was also a turning point in the life of my mother and my father, in their relation to one another and to their children. It was the episode of the violent and definitive destruction of a family of four, a destruction whose facts, twists and turns I was the first and the only one to establish forty-six years later by reading the correspondence of my parents and by recalling one or two lifeless memories, enigmatic but unyielding in their power, memories that I patiently examined and decrypted - long after my father’s and my mother’s deaths. It is not my purpose here to talk in depth about what I have learned and understood in the process of this lengthy undertaking, nor to discuss the meaning and the broader consequences of these events […] In December 1933, I recall being dropped off to live with a family of strangers, that neither I, nor my mother who brought me from Berlin, had ever seen before. In fact, these strangers who she left me to stay with were simply the first people she came across who agreed to take me on as boarder for a modest fee, and with no guarantee whatsoever that it would ever be paid. Meanwhile, my mother was about to join my father as soon as possible, who was impatiently waiting for her in Paris. [P.451]

After taking part in the Spanish Civil War, his parents returned to France in 1938 with a refugee status and reunited with their child (he was then ten years old). But in 1939 they were deemed “suspicious” because of their nationality and their activities: his father was first interned in the Vernet camp (Ariège), after which he was handed over to the Nazis by the Vichy authorities and would eventually die in Auschwitz; his mother was interned with her child at Rieucros camp (Lozère). From 1942 to 1944, young Alexander was hidden in Chambon-sur-Lignon at the"Cevennes College", administered by Pastor Trocmé who had been leading resistance efforts aimed at rescuing Jewish children.

During the last years of the war, when my mother was still interned at the camp, I was staying at “Secours Suisse”, a children’s home for refugee children at Chambon sur Lignon. Most of us were Jewish, and when we were warned (by the local police) that there would be raids by the Gestapo, we would hide in the woods for a night or two in small groups of two or three but did not think too much about how this behavior was meant to save our lives. The area was full of Jews who were hiding out in the Cevennes country, and the support of the local community helped many of them to survive. [P.32]

Alexander followed his studies in high school without considering himself to be one of the “brightest” students; actually, as a student, he tended to pursue his interests; this independent approach would stay with him in his later years.

Studying at a high school in Germany for the first year, and then afterwards in France, I was a good student, but not a “brilliant student.” I invested myself heavily in what interested me most, and tended to neglect what didn’t interest me as much, without worrying too much about the assessment of whatever teacher I happened to have at the time. In 1940, during my first year of high school in France, I was interned with my mother in the concentration camp of Rieucros near Mende. It was war, and we were foreigners - “undesirable elements” was the expression used at the time. But the camp administration looked the other way when it came to the kids at the camp, as “undesirable” as they were. We went in and out as much as we wanted. I was the oldest, and the only one to go to high school four or five miles away, rain or shine, with makeshift shoes that would always be filled with water. [P.32]

He graduated from the “Collège Cévenol” and became a student at Montpellier in 1945. Then the period of his scientific training began. From the outset Grothendieck surprised his elders. Working independently, he reinvented “the Lebesque integral” (which dated back to 1902) to calculate complex volumes.

In the mind of the two or three older colleagues with whom I discussed this effort (or to whom I even showed a manuscript), it amounted to wasting his time and simply “retreading old ground”. I do not remember being disappointed, either. At that time, the idea of enhancing my “reputation", whether that meant gaining the approval of others or getting them interested in the work I was doing, was not part of the way I thought. […] Without even knowing it, I learned by myself the core elements of a mathematician’s work - core elements that no teacher can really teach. Without having ever been told, without having ever met someone who shared my thirst for my knowledge, I think I still knew in my gut that I was a mathematician: someone who was working on math in the truest sense of the term - “making” math like “making” love. To me, mathematics was like a mistress who would always be open to fulfilling my desires. These lonely years have laid the foundation of trust that has never been shaken. [P.34]

After arriving in Paris in 1948, he soon leaves for Nancy where mathematicians of the internationally-renowned group “Bourbaki” [the name of an imaginary mathematician] such as Jean Dieudonné and Laurent Schwartz would train and mentor him as much as possible. Soon the disciple surpasses his masters: to test him, they give him fourteen problems that they have failed to solve. He can choose the problem that interests him the most… Dieudonné tells the story: “In less than a year, he had solved all our problems! ”

Recruited and promoted to the CNRS, he spent a few years abroad (in Sao Paulo) after completing his thesis. His return ushers in what will be his most productive period, stretching from 1958 to 1970, a period that coincides with the Bourbaki group’s best years. His lucky break came with the opening of the IHES institute [Bures-sur-Yvette Institut des Hautes Études Scientifiques] where he and Dieudonné were jointly offered a chair in mathematics. That’s where Grothendieck’s great adventure began. He led a prestigious seminar in which young talented mathematicians came together to make new discoveries and collaborated with great passion; he also initiated an ambitious project that aimed to fuse arithmetic and geometry.

In 1966, Grothendieck received the Fields Medal, which is the most prestigious award in recognition of accomplishments in mathematics and is often compared to the Nobel Prize. First sign of discontent though: Grothendieck boycotted the medal presentation ceremony, held in Moscow, to protest against Soviet military action in Eastern Europe.

The chasm widened in 1968: when the anarchist, libertarian Grothendieck addressed a group of students occupying the Orsay university, he discovered that he, a non-conformist, was seen by them as a “mandarin”! He came before them to defend scientific research; two years later, he abandoned the mathematical community by asking the question: “Will we continue to conduct scientific research?” He then returned to Montpellier, where he worked as a simple teacher up to his retirement - after he retired, he lived alone in a small village in the Pyrenees mountains where he died last year on November 13th.

II. Accomplishments in mathematics #

So how should we go about summarizing Grothendieck’s exceptional contribution to mathematics? - A contribution that will require perhaps decades to be fully assimilated by the following generations of mathematicians.

This contribution is the result of a truly comprehensive approach, the search for a full understanding that ignores the usually established boundaries between separate fields. The ambition of Grothendieck’s vision is to bring the two separate worlds of geometry and arithmetic together by developing what he proposes to call a new “arithmetic geometry”.

We can consider the new geometry to be primarily a synthesis between these two worlds, which were previously adjoined and closely connected, yet separate: the world of “arithmetic” that houses the (so-called) “spaces” without a principle of continuity, and the world of continuous magnitude, where “spaces live” in the true sense of the term, and where they are available to the tools of an analyst; for that very reason, the analyst accepts them as entities worthy of residing in the mathematical city. In the new vision, the two formerly separated worlds unite to become one. [P.50]

The title of his great work demonstrates the scope with which he wishes to endow his research. The title - Elements of Algebraic Geometry - pays homage to Euclid’s Elements of Mathematics by implicitly referring to it. This is nothing less than designing a new mathematics based on Euclid’s mathematics.

Crops and Seeds sees Grothendieck using his typical approach, citing metaphors as is his habit, metaphors such as those of a “home” to build, but also metaphors of heirs and of a builder.

Most mathematicians are likely to be confined within a conceptual framework, a “Universe” fixed once and for all - one they basically found as “complete” during their education. They are like the heirs of a great and beautiful fully-equipped house, with living rooms and kitchens and workshops, and cookware and tools in all corners, but in which you can still cook and tinker. How this house was gradually built over generations, and how and why such tools (but not others) were designed and crafted…), why the rooms are laid out and developed in a certain way here, but in another way there - these are all issues that the heirs would not dream to question. That’s “the universe”, the “given” in which one must live, and that’s all there is to it! It’s something that looks great (and they most likely haven’t even explored all the rooms), but familiar at the same time; but most of all it is immutable.

[…]

In my mind, I feel like I am part of a lineage of mathematicians whose spontaneous vocation and joy is constantly building new homes. Along the way, they also can’t help inventing and giving shape to tools, utensils, furniture and required instruments, not only for building the house from the foundation all the way up to the top, but also for copiously filling in future kitchens and future workshops, and furnishing the home to be able to live in it comfortably.

However, once everything to the last gutter and the last stool is set, it’s rare that the worker takes the time to linger in these places, where every stone and every rafter bears the trace of the hand that has worked on it and put it in place. His place is not in the tranquility of the ready-made universe, as welcoming and as harmonious as it is - it has been arranged by his own hands or by those of his predecessors. Other tasks in other places are already calling him, pressing urges (to satisfy needs) that he is the only one to feel; or perhaps he anticipates needs that he’s the only one to sense. His place is in the open air. He is a friend of the wind and is not afraid to be alone with his task. [Pp.38-39]

Grothendieck continues, providing us with his own interpretation of his work as a mathematician:

If I excelled in the art of the mathematician, this wasn’t so much because of my skills and my determination to solve problems left to me by my predecessors, but rather due to my natural tendency to pick up on crucial issues that nobody else had noticed, or to identify the “best ideas” that were missing (when the new concept hadn’t yet been proposed, no one realized that it was missing) and good formal elaborations which nobody had thought of before.

[…]

But more than just simply discovering new questions, ideas, and formal elaborations, my gift lies in the discovery of groundbreaking points of view and this talent has always driven me to introduce and develop completely new topics. And that, I believe, is essentially my contribution to the mathematics of my time.

[…]

But as its very name suggests, a “point of view” in itself is limited. It reveals to us only one view of a landscape or a panorama, among a multiplicity of others that are equally valid and real. “It is when these complementary points of view of the same reality are combined, when our ability to view things is enhanced, that the view can provide us with a more complete access to the knowledge of things. The more complex and rich the reality we want to grasp, the more important it is to have several "sets of eyes” to apprehend it to its fullest extent and in all its finesse.

And it happens sometimes that a beam of convergent views on the same vast landscape enables us to grasp the One through its multiplicity, gives birth to something new: a whole that surpasses each partial perspective, just as a whole organism is more than a sum of its body parts and organs. We can simply refer to this new thing as vision. Vision unites the already known points of view that embody it as well as revealing others that were previously ignored, just like a groundbreaking perspective enables us to understand and discover that a multiplicity of issues, concepts and new formal elaborations are in fact a part of the same whole. [pp.41-43]

The unifying vision of Grothendieck has led him to define a common framework to simultaneously study the geometric (“continuous”) and the arithmetic (“discrete”) aspects of Mathematics that challenge the idea of space. We therefore compared Grothendieck to Einstein. Grothendieck made the comparison himself, not to invoke, but to underline both the kinship of spirit and the difference in “substance” between him and Einstein, since Einstein’s work was in the field of physics, while his own was in mathematics:

The idea of comparing my contribution to the mathematics of my time with Einstein’s contribution to physics came to me for two reasons: First, both of our accomplishments rely on the transformation of our conception of “space” (a mathematical conception in my case, but a conception of physics in his); and both take the form of a unifying vision that encompasses a wide variety of events and situations that previously seemed unconnected. I think that the spirit of my work and his work are indeed related.

[…]

This relationship seems to me in no way contradicted by an obvious difference in “substance”. As I have already hinted earlier, Einstein’s transformation affects the concept of space in physics, as Einstein draws on the arsenal of previously-discovered mathematical concepts and doesn’t need to expand it, or turn it upside down. His contribution was to identify the mathematical structures of his time that would best help him model the world of physical phenomena to replace the defunct models inherited from his predecessors. Thus he was engaged in the work of a physicist, but on a deeper level, he was also a “natural philosopher” in the sense that the vocation was understood by Newton and his contemporaries. The “philosophical” character is missing from my mathematical work, since I was never driven to ask myself questions about the relationships between the ideal conceptual constructions taken from the mathematical universe and phenomena that occur in the physical universe (or even, experiences that take place in the psyche). I was purely exercising the role of a mathematician who decided to turn his attention away from issues such as applications (to other sciences), motivations, and the psychological roots of my work. Furthermore, my work in mathematics was driven by a very special talent to permanently expand the arsenal of concepts that formed the very basis of my discipline. This is how I came to revolutionize the most fundamental concept of all in geometry: space (and “variety”), i.e. our very concept of “place” that is home to geometric figures. [P.68]. I didn’t even realize what I was about to accomplish, it was more like playing a game.

Grothendieck reveals a lot about himself in the words “I didn’t even realize what I was about to accomplish, it was more like playing a game…” These words remind us of children’s games. In fact, for him, “creation” connects us to the inborn abilities of children who set out to discover the world by playing.

In our knowledge of the things of the universe (whether mathematical or otherwise), the power to innovate that lies within us is really nothing but innocence. It is the original innocence that we were all endowed with at birth, that lives inside all of us, but is often the object of our contempt and of our most secret fears. This innocence is what brings together the humility and the audacity that make it possible for us to get to the heart of things, but also allows things to deeply affect us and get under our skin so that they leave a lasting imprint on our minds and souls.

[…]

Discovery is a child’s privilege. I mean the small child, the child who is not afraid to be wrong, to look silly, to not be serious, and to act differently from everyone else. He is also not afraid that the things he is interested in are in bad taste or turn out to be different from his expectations, from what they should be, or rather he is not afraid of what they actually are. He ignores the silent and flawless consensus that is part of the air we breathe – the consensus of all the people who are, or are reputed to be, reasonable.

[…]

The child discovers the world just like he breathes - the ebb and flow of his breathing make him welcome the world into his delicate being, and allow him to open himself up to experience the world that equally receives him with open arms. The adult also discovers that he has new eyes, the eyes of a child, in those rare moments when he forgets his fears and his knowledge, when he is eager to learn and look at things or himself with wide-open eyes. [p.127].

To conclude this section, I will cite Grothendieck’s beautiful text about the creation of the world:

God was creating the world step by step as he discovered it, or rather he constantly creates the world as he discovers it - and he also discovers it in the process of creating it. He created the world and is still creating it day after day, restlessly correcting himself millions of millions of times, feeling his way around, making mistakes millions of millions of times, and ceaselessly making adjustments without wearing himself out.. Each time, as he probes into the nature of things, the way the things respond (“that’s not a bad try” or"you’ve got to be kidding,“ or "it’s working perfectly, keep going”), guides him towards new opportunities to either readjust the previous try or to simply keep at it in response to the previous answer… During each cycle of back-and-forth in this infinite dialogue between the Creator and Things, which takes place at every moment and in every place of creation, God teaches, discovers, learns about things in more depth while they form and change in His hands. This is apparently how the process of discovery and creation works, and how it has worked for all of eternity (that is as far as we can know eternity). This is what the process has been like only a million years ago or so, before man made his tardive appearance on the stage to get involved in it – an involvement that has brought many unpleasant consequences that we all know about. [P.128]

III. Break with the mathematical community: meaning and spirituality #

I mentioned earlier Rimbaud, another genius who, at the age of 21, left poetry to become an adventurer. The controversy of what to make of his abandonment of poetry will never be resolved. As for Grothendieck, he never really left mathematics behind (he continues to fill pages and pages of calculations even during his retirement… “boxes full of scribbles”), he left the “mathematical community”, disassociated himself from institutions devoted to the research and study of mathematics, resigned his position, his chair, and gave up his seminar… and instead involved himself in a quest for meaning.

What caused this break with the past? His colleagues recall the shock of an event from 1968: he was badly treated. "It was like a terrible slap in the face, it was so brutal; afterwards, he was no longer the same.” He ends his relationship with the founder of the IHES who accepted military funds to finance the institute. No more. He decides to get away and return to his home university, where he takes on the role of a simple teacher.

Two passages of Crops and Seeds deal with his departure from the institutions associated with mathematics:

As you know, in 1970 I isolated myself from the milieu where important and renowned mathematicians gathered, in response to an issue related to the use of military funds in my home institution (the IHES) After years of “cultural revolution” style anti-militarist and pro-environmental activism, which you’ve probably occasionally heard about, I almost completely disappeared from the scene, and was cloistered in a far-off provincial university located God knows where. Rumor had it that I was spending my time tending sheep and drilling wells. The truth is that, aside from the other activities that I was engaged in, I bravely taught my courses at the university (that was my original occupation and remains so today) and would even occasionally playfully tinker with math – I have boxes full of scribbles and I am probably the only one who can decipher them. [P.75]

Why did I abruptly make a break with a world in which I apparently felt comfortable for over twenty years of my life? I speak throughout the text of Crops and Seeds of the circumstances of my departure, but don’t dwell on them at length. This “departure” appears in the text as an important pause in my life as a mathematician - the events of my life as a mathematician are defined in relation to this point in time, either belonging to the “before” or the “after.” It took a powerful shock to tear me away from a community that I was deeply rooted in, and from a clearly-defined career path. The shock resulted from my confrontation with a certain type of institutional corruption in an environment that I closely identified with. I chose to close my eyes to this corruption (by simply abstaining myself from not participating in it). Looking back, I realize that beyond the specific circumstances of the event, deeper forces were at work within me. It was an intense need for inner renewal. The heated atmosphere of a prestigious institution was no place to nurture and support such a renewal.
I had twenty years behind me of intense mathematical creativity and extreme dedication to mathematics; but on the other hand, after twenty long years of being cut off from the world, I was mired in spiritual stagnation. I didn’t realize it, but I was suffocating – what I needed was a breath of sea air! With my auspicious departure, I put an end to my long stagnation, and took the first step towards balancing the forces in the depths of my being that were intertwined and fixed in a state of an intense and rigid imbalance. This departure was truly a new beginning - the first step on a new journey.

Grothendieck’s colleagues did not understand this departure. Many spoke of “suicide”; others of “desertion”; some believed “the man is lost to math,” “the machine is out of order “. As for his students, (including his disciple Pierre Deligne, a future Fields Medal recipient), they had to face the daunting task of taking it upon themselves to continue exploring along the paths that were opened to them by Grothendieck, as the visionary himself was no longer there

This abrupt departure marks a major break in his life as a mathematician. It seems that what triggered it was the disagreement with the founder of the IHES who accepted military funding for the institution. From this point on, Grothendieck’s political awareness comes to play a much more important role in his life; this political awareness was already there before, but assumes its full power only now. As he starts to rethink his past in the world of mathematics, he comes to discover the flaws, the compromises, and the ethical issues at play in this milieu. As he unravels and analyzes all of these, he makes no concessions, even going as far as to pose the harsh question, "Will we continue to conduct scientific research?”, in front of an audience of CERN scientists.

`
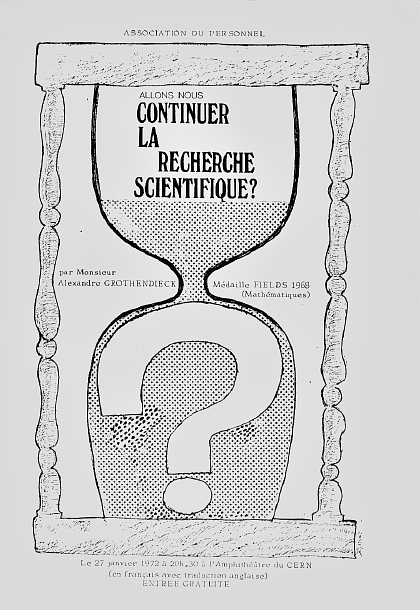
Leaflet announcing the conference at CERN January 27, 1972

In fact, this iconoclastic question represents his attempt to grapple with the issues that are at stake of what came to be called “political ecology”. Grothendieck identified with this movement; at the time, he became involved as an activist in the group “Surviving and Living”.

“Surviving and Living” (which was originally only called “Surviving”) is the name of a group that initially advocated for peace, but then later also advocated for the preservation of the environment. The group was started in July 1970 by scientists, many of them mathematicians, at a “Summer School” at the University of Montreal. As it grew, it came to focus on “cultural revolution" and was no longer limited to scientists but increased its reach to a broader public. Its main means of action was a newsletter, which was named after the group and was released more or less periodically. The group’s directors, listed in chronological order, were Claude Chevalley, myself, Pierre Samuel, Denis Guedj (all four were mathematicians). There was also an English-language edition that was maintained thanks to the hard work of Gordon Edwards (a young Canadian mathematician whom I had met in Montreal and who was also one of the initiators of the group and the newsletter).

I wrote the first newsletter completely by myself (I was naive and full of conviction! ) A thousand copies were printed and distributed at the International Congress of Nice (1970), which brought together thousands of mathematicians (once every four years as always). I was expecting lots of people to join the group- if I remember correctly, only two or three did. I became aware that my colleagues were very uncomfortable about it! By speaking about the collaboration between scientists and the military apparatus, which had infiltrated every aspect of the scientific work in academia, I deeply embarrassed the listeners… I was particularly troubled by the reception I received from the important and influential mathematicians; few had connected with my message; Chevalley and Samuel were among those few. Our action did have a certain resonance in the backwaters of the scientific world.

It’s in what I have elsewhere called “the swamp” of the scientific world that our action has found a certain resonance. We ended up printing fifteen thousand copies, an impressive accomplishment in terms of logistics, and the distribution was handled traditionally without any sophisticated methods.(P.622)

The message was simple: this planet is going to die soon, we need to completely change our way of life. Grothendieck changed his lifestyle completely. After leaving behind his chair and his seminar, he became a simple teacher at his former high school in Montpellier, where he continued to teach until his retirement. He had also settled in a small village where he led a reclusive life and lived close to nature, devoting himself to what he called “meditation.”

Actually, his vision of himself didn’t change overnight, he says. It took a few years to begin to get to know himself and get into meditation.

My attempts to reconsider my ideas (such as the “social role of the scientist”, of science, and so on…) that I had come to either on my own or had been driven to by the logic of reflection or by my activities in the group “Surviving” – these attempts to reconsider and reevaluate ideas remained mainly superficial. Of course, they touched on the world in which I lived and on the role that I played there - but they didn’t really affect me profoundly. My vision of my own person did not change a bit during this intense period of my life. That is not when I started to get to know myself. It is only six years later that for the first time in my life I freed myself of a persistent illusion, an illusion that wasn’t about others or the surrounding world but that was related to myself. It was another awakening, with an impact even greater than the one from which it arose. It was one of the first of many successive awakenings, and I hope more will come in the years that I have left.[P.144]

In 1976 a new passion appeared in my life, whose power could only be compared to my passion for mathematics of a previous era; indeed, it was closely related to it. It is the passion for what I called “meditation” (we do have to name things after all). This word, as would any other word here, will undoubtedly give rise to countless misunderstandings. As in mathematics, this is a work of discovery. I speak about it throughout the text of Crops and Seeds. [p.75]

Crops and Seeds can confuse readers. There are a lot of thoughts, observations, and analyses that seem like they are replayed in a loop, because they are constantly repeated, reiterated, and re-examined in increasing depth. The text can be compared to a sieve that keeps the substance being sifted as a whole, and yet separates the elements making up the mixture. This is the background against which Grothendieck’s meditation is carried out until the truth and meaning of events past and present are extracted. It is what Crops and Seeds is all about.

There are many aspects to Crops and Seeds and each reader will come away with a different take on its content: a trip to discover the past; a meditation on existence; a description of the ethics and customs of a milieu and an era (or a description of the insidious and relentless shift from one era to another…); an investigation (almost police-like at times, and other times resembling a cloak-and-dagger novel about seedy happenings in a mathematical megalopolis…); extensive mathematical digressions (there’s more than one); a practical treatise on applied psychoanalysis (or alternatively, a book of “psychoanalytic fiction”); an encomium to self-knowledge; “My Confessions”; a diary; a psychological account of discovery and creation; an indictment (ruthless, as it should be…), or rather an attempt to settle his scores with the “beautiful mathematical world” (and he makes no gifts there… ). What is certain is that I was never bored when writing it; on the contrary, I learned much from the process and dealt with some challenges as well.

It is impossible to exhaustively cover or to even simply give an overview of everything that is discussed in his deep meditative confession whose pages are overflowing with ideas. I will only mention what Grothendieck defines as two types of corruption in his former work environment. The first one prompted his departure from the mathematical scene: the self-serving collusion of scientists with the military establishment. He discovered the second type of corruption almost fifteen years later, when he wrote Crops and Seeds: the plagiarism of his work by those who appropriated his results without even citing him or ever mentioning his name - he speaks of Burial, Funeral. His meditation on these events gave him the feeling that these two types of corruption are not unrelated. He realized that what unites them is the lack of self-respect; and it is in the loss of self-respect that he recognizes the root of the loss of respect for others, and for the work of the Creator - the disrespect of nature, the disrespect of the environment.

I see that these types of corruption, both the type that caused my departure and the type that was waiting for me as I returned are not unrelated. If I try to define in words this vague feeling of a connection between them, I would say that I have discovered a lack of self-respect, both among individuals and society as a whole, in how comfortable scientists are with succumbing to the temptation of receiving money from the military establishment (to mention only that aspect) along with benefiting from the convenience that this money offers. And I also recognized that the lack of self-respect lies at the root of the loss of respect for others and for the living creation that comes from their hands or from the hands of God. I do not claim to have “understood” either type of corruption. There is on the one hand the “spirit of the times”, the particular dynamics that are largely beyond the actions of individuals. This collective dynamic remains a complete mystery to me that I’ve never thought about trying to pierce. On the other hand, there is a way in which each individual endowed with his faculties of perception and creativity, but also burdened by the weight of his particular conditioning, confronts this spirit of the time and allows this confrontation (knowingly or not) to become a crucial element of his individual journey. [p.911]

Grothendieck withdrew from the scene in order to not even passively condone corruption, but he did not abandon his work. For that reason his dismay at the plagiarism that goes on among his former students has only grown. But as a result of his self-development, he has added the following remarks:

If Crops and Seeds, which was primarily a reflection on my past as a mathematician, has had a meaning, it was to help me understand, among other things, that even if some who were my students have disavowed me, it is not for me to disown any of them. What I reap from them is part of the crop that I have helped to sow, just as they themselves had their part in it too. And this realization that I commit to words with an uncompromising pen is not an indictment of anyone, but rather an observation that involves me as much as any of them. [P.709]

Crops, sowing: you reap what you sow, you cannot shirk responsibility - this awareness is part of the long work of self-discovery that he initiated by deciding on his departure, a decision that was insane according to his fellow mathematicians.

With my auspicious “departure,” I put an end to my long stagnation, and took the first step towards balancing the forces in the depths of my being that were intertwined and fixed in a state of an intense and rigid imbalance. This departure was truly a new beginning - the first step on a new journey.

“It is said that the world becomes fertile with any decision where we express ourselves fully: there where winter soil stretched out as far as the eye could see, a thousand possibilities rear their heads and turn it green.” [Gracq, The Lands of the Setting Sun]

CERN conference on January 27th, 1972